
Članak je napisan 25.11.2014. Dodatno je uređen 23.01.2020.
Biste li radije 1.000 € danas, ili 1.000 € za godinu dana?
Kakvo je to pitanje, pa naravno da bismo radije 1.000 € danas.
I da, ako ste upravo pomislili da gotovo svaki tekst koji se bavi vremenskom vrijednošću novca počinje upravo s tim pitanjem, u pravu ste.
Ono što namjeravam ovdje postići je razjasniti temu čitateljima koji se nikada nisu sreli s njom, te biti od pomoći studentima koji se upravo hvataju ukoštac s ovim gradivom.
No prije svega, idemo odraditi formalnost i napisati definiciju:
Što je vremenska vrijednost novca?
Vremenska vrijednost novca (eng: Time Value of Money) koncept je koji kaže da novac dostupan u sadašnjem vremenu vrijedi više od identičnog iznosa u budućnosti zbog svoje potencijalne mogućnosti zarade. Ovo temeljno načelo financija drži da, pod uvjetom da novac može zaraditi kamate (veće od inflacije), svaki iznos novca čim je prije primljen, tim vrijedi više.
Šefe, može to malo jasnije?
Ma naravno da može! Jednostavno, ako danas imamo 1.000 €, možemo ih odmah potrošiti, ali isto tako ih možemo i oploditi, i u tih godinu dana bismo zaradili na njima, kroz kamate, dionice, biznis ili drugu imovinu kojoj raste vrijednost.
Kad bismo tih 1.000 € čekali godinu dana umjesto da ih odmah uzmemo, imali bismo izgubljenu dobit odnosno stvorili bismo oportunitentni trošak – sve ono što smo mogli s njima napraviti i zaraditi, a nismo.
Tu je i inflacija. tih 1.000 € danas vrijedi više nego za godinu dana. Ako je inflacija 2% godišnje to je 19,61 €! [1000/1,02=19,61], dakle imali bismo 980,39 € u kupovnoj vrijednosti.
Očito imamo hrpu argumenata zašto je bolje imati istu količinu novca danas nego za godinu dana.
Novac koji stoji neupotrjebljen, biva izjedan oportunitentnim troškom i obezvrjeđujućim faktorom inflacije. Iz tog razloga financijski eksperti govore tvrtkama da je gotovina financijska obveza (cash is liability), i kompanije koje drže puno keša na računu smatraju se neefikasnima. Barem je tako bilo prije krize. Kompanije su u vrijeme krize spremne držati novčane rezerve unatoč velikom trošku. (Naravno, ne govorimo o 1000 €, već o milijunima, gdje se to itekako osjeti).
No, vratimo se na našu priču o 1000 €.
Ako vas pitam da li biste radije 1.000 € danas, ili 1.500 € za godinu dana, e tu već nastaje problem, jer ne znamo koji bi nam od ta dva odgovora donio više novca. Odgovor je zapravo – “ovisi”.
Tih 1.500 € bi uz inflaciju od 2% za godinu dana vrijedilo 1.470,60 €, ali da pojednostavimo stvar i koncentriramo se samo na vremensku vrijednost novca, inflaciju više nećemo spominjati.
Ono o čemu naš odgovor ovisi je kamatna stopa. U ovom primjeru je jasno da 50% nećemo dobiti niti u banci niti na iole sigurnijim financijskim tržištima. Osim ako nismo u nekom prilično dobrom biznisu, vjerojatno je bolje 1.500 € uzeti za godinu dana.
No stvari tu znaju biti dosta kompleksnije…
Na primjer, pitanje može glasiti:
Ako uložimo 100 € po 10%, koliko ćemo imati nakon godinu dana?
Jednostavno: 100 * 1,10 = 110 €.
Dobro, to nije bilo tako teško… Ali što ako ih uložimo na 2 godine?
100 € * 1,10 * 1,10 = 121 €.
A na 3 godine?
100 € * 1,10 * 1,10 * 1,10 = 133.10 €.
4 godine su 146,41 €, i tako dalje.
Malo je naporno pisati toliko puta za redom “* 1,10”.
Što bi tek bilo da moramo računati za npr. 30 godina. Mora postojati neki bolji način.
I ima ga, a to nas dovodi i do naše prve formule, iliti formule 1. (Hmmm, ovo nije bilo namjerno).
![]()
Da vam budem iskren, meni se ova formula gore nimalo ne sviđa. Zapravo, nije da mi se ne sviđa, već se malo previše naglo pojavila u čitavoj ovoj priči, i statistički prestrašila 78,2% ljudi koji su je ugledali. [lažem oko statistike, ali kladio bih se da je to tu negdje].
Idemo mi tu formulu razmontirati na dijelove, k’o klinac formulu na daljinsko upravljanje, shvatiti svaki djelić, i tek tada krenuti dalje.
No za početak, upoznajmo se s pojmovima:
| OZNAKA | ENGLESKI NAZIV | HRVATSKI NAZIV | ALT. OZNAKE |
| FV | Future value | Buduća vrijednost | – |
| PV | Present value | Sadašnja vrijednost | – |
| k | Interet rate | Kamata | r “i” “i/YR” |
| A | Annuity | Anuitet | PMT (Payment) |
| n | number of compounding time periods | Trajanje | t |
Dosta za sad.
Vrijeme je da razbijemo ovu formulu gore, koja daje odgovor na pitanje kolika je…
Buduća vrijednost novca
Kad sam radio vremenske lente koje slijede, pisao sam u dolarima. Nemojte mi zamjeriti što od sad na dalje napuštamo Eure.
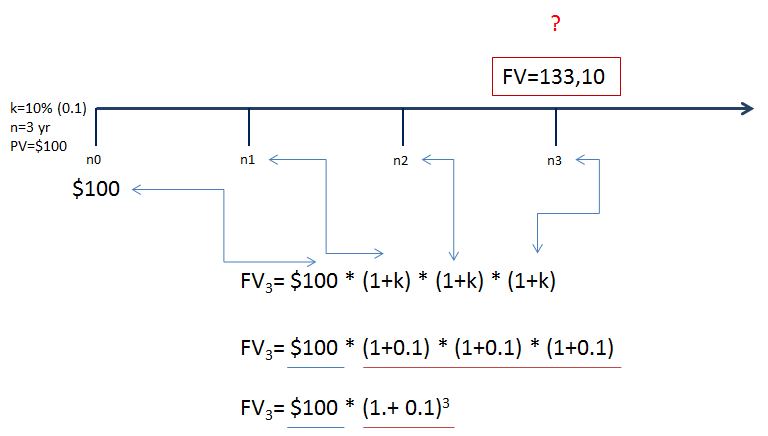
Dakle pitanje je, koliko ćemo novca imati [u budućnosti] ako danas uložimo 100 dolara na trajanje od tri godine, uz kamatu od 10%?
Poznato nam je sljedeće:
k = 10% (Prikazujemo kao 0,10)
n = 3 godine
PV = $100
Rekli smo da to bez formule računamo na sljedeći način:
$100 * 1,10 * 1,10 * 1,10 = $133,10.
Prvi dio je jasan, “$100” predstavlja PV (Present Value), tj sadašnju vrijednost novca kojeg imamo u džepu. [Zanima nas buduća vrijednost].
Tri puta za redom smo pomnožili s 1,10, zato što je trajanje tri godine, dakle n=3.
1,10 je tu zato što se radi o kamati od 10%. Daje bila 8%, pisalo bi 1,08. To je broj s kojim množimo sadašnju vrijednost da bismo dobili vrijednost nakon jednog perioda ukamačivanja [Npr. nakon jedne godine].
Kasnije ćemo 1,10 u formuli prikazivati kao 1+0,1.
Slikoviti primjer:
100 * 1,10 = 110.
Kad na 100 dolara pripišemo 10% kamate, dobijemo 110 dolara.
To je to.
Idemo sad to pretvoriti u proširenu formulu, pa ćemo je polako dotjerati do one gore što prestraši 72,8% ljudi.
FV = $100 * (1+k) * (1+k) * (1+k)
Rekli smo da ćemo 10% kamate (k) prikazati kao 0,1, jer formule baš ne vole prikaz u obliku postotaka. Pa evo:
FV = $100 * (1+0,1) * (1+0,1) * (1+0,1)
Sad dolazimo do ključnog dijela. Primječujemo da smo (1+0,1) ponovili (pomnožili) tri puta za redom, jer je trajanje tri godine. Da je trajanje bilo 30 godina, to bi već bila kobasica za svjetski rekord, jer bismo te zagrade ponavljali 30 puta za redom. Umjesto toga, jednostavno kažemo (1+0,1) na treću. Unutar teksta ćemo za dizanje na potenciju koristiti znak “^”, npr: (1+0,1)^3.
Da je trajanje bilo 30 godina, rekli bismo (1+0,1) na tridesetu, i spasili bismo šume od prekomjernog korištenja papira uzrokovanog silnim ponavljanjem jednog te istog.
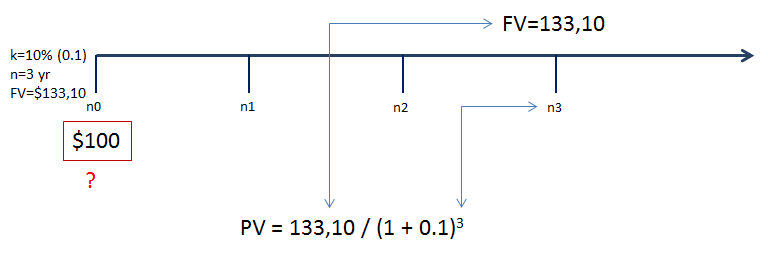
Idemo sad na vremensku lentu. n1, n2 i n3 predstavljaju oznake za prvu, drugu i treću godinu. N0 [En nula] predstavlja današnji dan, tj. nultu godinu odnosno sadašnju vrijednost ($100).
Buduća vrijednost koju tražimo nalazi se na n3, odnosno u trećoj godini.
Na kraju smo došli do formule FV (za tri godine) = $100 * (1+0,1)^3.
Usporedimo sad to s formulom s početka:
Formula: buduća vrijednost novca
Više nije tako strašna, zar ne?
FVn (Buduća vrijednost u godini “n”) jednako je PV0 (Sadašnja vrijednost) * (1+kamata) na entu, gdje “n” predstavlja trajanje, odnosno broj ukamaćivanja.
Možda sam za neke pretjerao s objašnjavanjem, ali smatram da je ovo razbijanje formule na proste faktore jako važno, kako bismo razumjeli samu srž kalkulacije vremenskog tijeka novca, čak i ako nismo matematičari.
Razumijevanje na ovoj temeljnoj razini bitno će nam olakšati ostale TVM kalkulacije (Time Value of Money), odnosno vremenska vrijednost novca. Kao što ćemo vidjeti, sve se vrti više-manje oko istog koncepta.
Sadašnja vrijednost novca
Izračunali smo da 100 dolara sada, uz kamatu od 10%, za tri godine vrijedi 133,10 dolara.
A što ako znamo da za tri godine želimo imati 133,10 dolara, te nas zanima koliko moramo uložiti danas, uz kamatu od 10%, da bismo došli do tog cilja?
Znam da znate odgovor, 100 dolara, jer je to naopaka formula od maloprije. Ali kako je prikazati?
Jednostavno:
Formula: Sadašnja vrijednost Novca
Sadašnja vrijednost jednako je buduća vrijednost / (1+k)^n.
Sad kad smo temeljito razbili prvu formulu, mislim da ova više ne djeluje tako grozno.
Idemo odmah na vremensku lentu:
Znamo kamatu (10%), trajanje (3 g.) i buduću vrijednost ($133), a trebamo sadašnju vrijednost u godini n0. Formula je vrlo jednostavna i jasna. Rezultata je u crvenom kvadratu i iznosi $100.
Studenti, ne dajte da vas profesori zavaraju ako vam pokažu malo drugačiju formulu. radi se o istoj stvari:
Alternativna formula: sadašnja vrijednost novca
Ako vam zatreba formula za izračun kamate, ide ovako:
Formula: kamata, sadašnja vrijednost novca
Buduća vrijednost anuiteta (uplata na kraju perioda)
Do sad smo se bavili jednokratnom uplatom. Ali što ako svake godine uplatimo po 100 dolara?
Ovdje trebamo razlikovati dva scenarija, uplate možemo izvršiti u nultoj, na početku prve i na početku druge godine, ili možemo početi s uplatama od kraja prve godine na dalje, te ostale anuitete uplaćujemo na kraju druge i na kraju treće godine.
Ako počnemo s uplatama odmah, onda se to zove annuity due tj. uplata na početku perioda. Ali idemo prvo vidjeti slučaj kad se uplata vrši na kraju perioda, tj. Ordinary annuity.
Formula ide ovako:
Formula: buduća vrijednost anuiteta na kraju perioda
Poznato je sljedeće:
k=10% (0,1)
n=3 g
A=$100
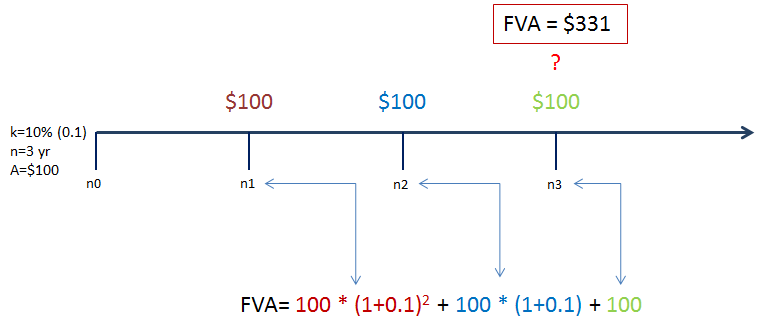
Dakle godišnji anuitet je 100 dolara, ali prvi anuitet dospijeva tek na kraju prve godine.
To u praksi znači da će se prvi anuitet stići ukamaćivti dva puta, i to od prve (ne nulte) do treće godine.
Drugi anuitet će se stići ukamatiti samo jednom, i to od druge do treće godine.
Treći anuitet se neće stići ukamatiti uopće, jer je to kraj perioda. Trajanje je bilo na tri godine.
Idemo sad na lentu:
Lijepo se vidi da je to zapravo prva formula koju smo upoznali (buduća vrijednost), ali izračunata za svaki anuitet zasebno, i na kraju zbrojena.
Svaki sljedeći anuitet ima sve manje vremena pred sobom, jer se približava trećoj, završnoj godini.
Zadnji anuitet označen zelenom bojom ne množi se ni sa čim, jer nema daljnjeg ukamaćivanja.
Jednostavno, zar ne?
Buduća vrijednost anuiteta (uplata na početku perioda)
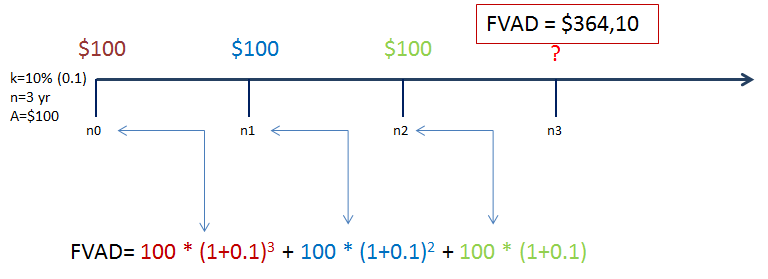
Za razliku od uplate na kraju perioda koju smo prethodno obradili, sad imamo situaciju gdje prvu ratu uplaćujemo odmah u nultoj godini. To je očigledno bolje rješenje, jer kod trajanja od tri godine, prva rata će se stići ukamaćivati tri puta.
Druga rata će se ukamatiti dva puta a treća jedan put, jer je u trećoj godini kraj [Ukamaćuje se jer je uplaćena na početku treće godine, a ne kao u prijašnjem primjeru na kraju].
Jasno je da je zbog toga u ovoj varijanti veća zarada. U Prvom izračunu gdje je prva rata sjedala na kraju prve godine, imali smo $331, a sad ćemo dobiti $364,10.
Da ne duljimo, ovo su formula i lenta:
Formula: buduća vrijednost anuiteta, uplata na početku perioda
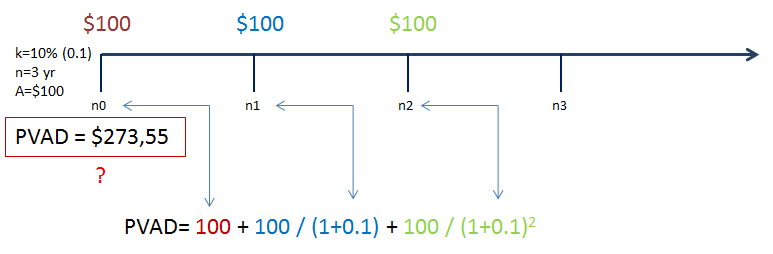
Sadašnja vrijednost anuiteta (uplata na kraju perioda)
Vrijeme je da s Čajne kobasice pređemo na Mortadelu. Ove formule su naizgled duže i kompliciranije, a zapravo smo to sve već vidjeli prije, samo što je sada drugačije posloženo.
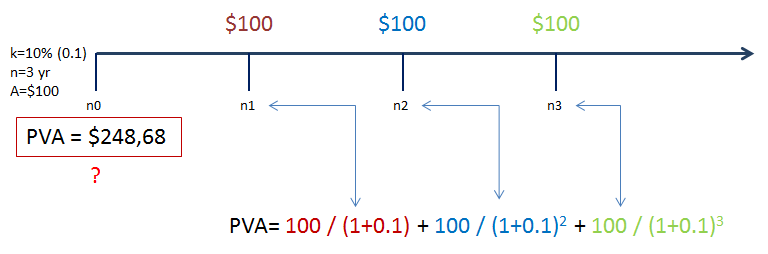
U ovom primjeru znamo da imamo tri uplate po 100 dolara godišnje, i znamo da je kamata 10%. Zanima nas kolika je sadašnja vrijednost tih (budućih) uplata.
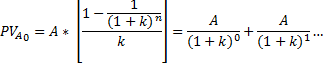
Formula: sadašnja vrijednost anuiteta
PVa0 predstavlja oznaku za sadašnju vrijednost anuiteta u nultoj godini. Vidimo da je to zapravo Anuitet kroz (1+k) na nultu + Anuitet kroz (1+k) na prvu + Anuitet kroz (1+k) na drugu + Anuitet kroz (1+k) na treću… i tako dalje.
Alternativna formula koja radi isto to, ide ovako:
Alternativna formula: sadašnja vrijednost anuiteta
Evo i lente:
Mala napomena za sve -ne-matematičare:
u formuli smo imali 100/(1+0,1)^2.
Ista stvar se može prikazati i ovako: 100 * (1+0,1)^-2
TVM formule znaju se prikazivati na oba načina, pa je dobro znati da je riječ o istom.
Evo formule za anuitet, kad je poznata sadašnja vrijednost:
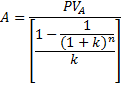
Formula: anuitet kad je poznata sadašnja vrijednost
Ovo je formula za anuitet kad je poznata buduća vrijednost:
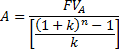
Formula: anuitet kad je poznata buduća vrijednost
Sadašnja vrijednost anuiteta (uplata na početku perioda)
Sve po starom:
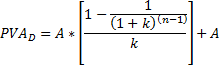
Formula: sadašnja vrijednost anuiteta, uplata na početku perioda
Alternativna formula:
Alternativna formula: sadašnja vrijednost anuiteta, uplata na početku perioda
Lenta:
Formula za anuitet, kad je poznata sadašnja vrijednost anuiteta s uplatom na početku perioda:
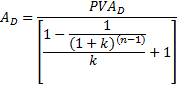
Formula: anuitet, poznata sadašnja vrijednost na početku perioda
Formula za anuitet kad je poznata buduća vrijednost:
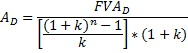
Formula: anuitet, poznata buduća vrijednost na početku perioda
Pravilo 72
Ovaj trik koristimo da bismo od oka, na brzinu procijenili koliko nam treba vremena da udvostručimo ulog, uz poznatu kamatnu stopu:
Dakle, ako imamo kamatu od 8%, da bismo udvostručili novac treba nam 72/8% = cca 9 godina.
Sadašnja vrijednost kontinuirano-rastućeg prihoda
Dobar primjer primjene ove formule je pokretanje biznisa, kad očekujemo da će prihodi “CF (Cash-flow)” kontinuirano rasti po stopi “g”, uz kamatnu stopu “k”, na “n” godina.
Alternativna formula: sadašnja vrijednost uz kontinuirani rast prihoda
Neto sadašnja vrijednost (NPV)
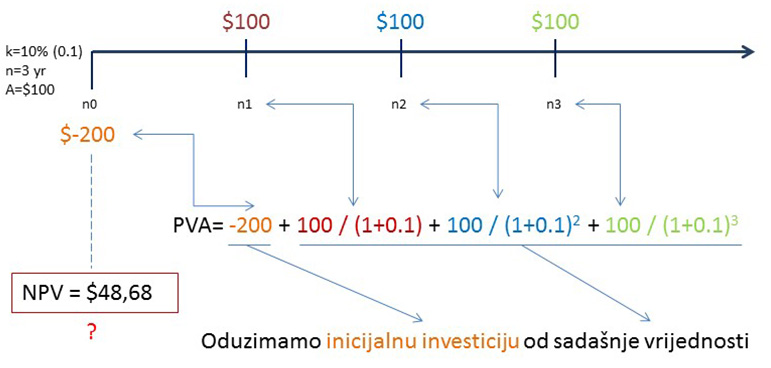
NPV (Net Present Value), je izuzetno korisna kalkulacija, naročito za pokretanje biznisa. U svojoj biti, NPV nije ništa drugo doli sadašnja vrijednost budućih prihoda (PVa0), od kojih je oduzeta inicijalna investicija u nultoj godini (-C0).
Ovaj veliki zastrašujući znak koji liči na slovo E nije ništa drugo do simbol za sumu. U ovom slučaju sumu svih diskontiranih prihoda, za svaku sljedeću godinu zasebno.
Ovdje je trajanje označeno s “t”, a kamatna stopa s “r”.
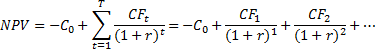
Formula: neto sadašnja vrijednost (NPV)
Bit će sve puno jasnije na lenti.
Uložili smo 200 dolara na početku, i tri godine za redom imamo prihod od 100 dolara.
Logično bi bilo da ako smo uložili 200 dolara, a zaradili 300 dolara, da je zarada razlika od 100 dolara. To je neto vrijednost.
Ali kalkulacija koja gleda samo na neto vrijednost nije u cijelosti točna.
NPV, odnosno neto sadašnja vrijednost nam pokazuje da je zarada zapravo 48,68 dolara, i to bez inflacije uzete u obzir.
Pogledajmo na lenti:
Ovdje je NPV pozitivan, dakle bez obzira što zarada nije kao što je izgledala, ipak je iznad nule, dakle biznis se isplati.
No NPV zna biti i negativan, iako je biznis na prvi pogled izgledao profitabilan…
Na primjer, ako smo nekome posudili $100 uz obećanje da će nam za godinu dana vratiti $105, neto vrijednost transakcije je $5.
Ako na trenutak zamislimo da je kamata u banci 6%, i napravimo NPV kalkulaciju, dolazimo do sljedećeg:
-100 + 105/(1+0,06) = -100 + 99,05 = -0,94
Dakle, ne samo da nismo zaradili $5, već smo još i izgubili $0,94! [Jer smo hipotetski novac mogli staviti u banku po 6%.]
Ako na vremensku lentu u nultu godinu stavimo iznos kompletne investicije, a na pojedine godine svu predviđenu zaradu i troškove [Troškove označavamo znakom minus], NPV će nam reći da li se investicija isplati. Ako je negativan, ne isplati se.
Naravno, preduvjet je da dobro procijenimo kamatne stope, prihod i troškove. NPV ima svoje mane zbog nagađanja, ali bolje imati nekakav plan nego nikakav…
Ako želimo izračunati neto buduću vrijednost, jednostavno prvo izračunamo neto sadašnju vrijednost, i nakon toga upotrijebimo formulu za buduću vrijednost (FV), te u njoj NPV uvrstimo umjesto sadašnje vrijednosti (PV).
Interna stopa rentabilnosti (IRR)
Internal Rate of Return, ili Interna stopa rentabilnosti (profitabilnosti) ima nepotrebno kompliciranu definiciju, pa ćemo je preskočiti. 😉
Prije nego se bavimo internom stopom rentabilnosti, idemo na trenutak baviti se stopom rentabilnosti.
Stopa rentabilnosti nije ništa drugo doli brzina povrata uloženih sredstava, a mjeri se u postotku po godini (%/god).
Postotak uzimamo od investicije, tj. uloženih sredstava.
Npr, uložimo li $100 danas, i na njih dobivamo $5 svake godine zauvijek, povrat je 5% godišnje. Dakle stopa rentabilnosti je 5%. [NE interna stopa rentabilnosti].
No što ako danas uložimo $100, i samo dvije godine za redom dobijemo $60, i iza toga nema više? Kolika je stopa povrata? 60% godišnje? NE!
Stopa povrata u ovom slučaju nije uočljiva iz prve, pa je stoga zovemo interna. [I zato što ne uključuje vanjske faktore poput inflacije, bla, bla].
Kao i kod prethodno objašnjenog NPV-a, imamo početnu investiciju koju označavamo s -100, i iza toga po dva diskontirana prihoda od po $60.
Zapravo ovdje pričamo o NPV-u s nepoznatom kamatnom stopom “r”, a ta nepoznata kamata je IRR.
-100 + 60*(1+r)^-1 + 60*(1+r)^-2
“r” je ovdje IRR.
Mogli smo isto prikazati i kao 60/(1+r)^2, ali Običaj je IRR formulu pisati na ovaj način. Također je ovdje kamatu primjerenije označiti s “r”, nego s “k”.
Da bismo pronašli IRR, moramo koristiti jednadžbu, odnosno čitavu gornju formulu izjednačiti s nulom, tj. tražimo koja bi to kamatna stopa donijela NPV jednak nuli. [Zato da bismo doznali koja je minimalna prihvatljiva kamatna stopa].
0 = -100 + 60*(1+r)^-1 + 60*(1+r)^-2
ALI, ako bismo krenuli rješavati jednadžbu klasičnom algebrom, varijable na jednu stranu, konstante na drugu stranu jednakosti, ne bismo dobili točan rezultat!
Pažnja, neki Youtube pametjakovići IRR objašnjavaju kroz Algebru. Ako to ugledate, bježite.
Zapravo, ovu jednadžbu je nemoguće riješiti!
Jedino što možemo učiniti jeste nagađati koliki je “r”, i metodom pokušaja i pogrešaka doći do rješenja.
Ili možemo koristiti Excel koji će umjesto nas nagađati dok ne pogodi, ali kudikamo brže. 😉
Idemo sad pretpostaviti da je IRR 14% (0,14). Uvrstiti ćemo to u našu formulu:
-100 + 60*(1+0,14)^-1 + 60*(1+0,14)^-2 = 0
=
-100 + 60*(1,14)^-1 + 60*(1,14)^-2 = 0
-1,2 = 0
Očito da -1,2 nije isto što i nula. Stoga moramo uzeti neku drugu kamatnu stopu.
Sad ćemo pretpostaviti da je IRR 12% (0,12). Uvrstiti ćemo to u formulu:
-100 + 60*(1+0,12)^-1 + 60*(1+0,12)^-2 = 0
1,4 = 0
1,4 nije jednak nuli.
Sad ćemo probati s nečim između, 13%:
-100 + 60*(1+0,13)^-1 + 60*(1+0,13)^-2 = 0
0,09 = 0
Ovaj rezultat je umalo pogodio nulu. Uglavnom se ovo smatra dovoljno preciznim, te možemo konstatirati da je IRR = 13%.
I što sad s tim podatkom?
Sad moramo usporediti IRR s najmanjom relativno sigurnom kamatom koju možemo dobiti u istom vremenskom periodu.
Ako ona iznosi 8%, a IRR je 13%, onda se definitivno isplati uložiti u projekt.
Ili…
dobiveni rezultat uspoređujemo s kamatom koju dajemo banci za posuđenih $100. Ako banci dajemo 8%, a IRR na uloženih $100 je 13%, tada smo 5% u plusu.
Nedostatak IRR-a je što ništa ne govori o iznosima. Da vas netko pita “želiš li uložiti u jedan odličan projekt? Ima IRR od 25%!”. Što biste mu odgovorili?
Pitali biste ga kolika je investicija, jer navedeni IRR vam može donijet 100 € ili 10 mil. eura, ili nešto treće.
Diskontiranje češće od godišnjeg
Do sad smo stalno radili godišnje intervale diskontiranja. Što ako primjerice nisu godišnji, već mjesečni? Ili polugodišnji ili kvartalni?
Rješenje je vrlo jednostavno, i vrijedi za sve formule koje smo do sad prošli.
Idemo vidjeti FV na primjeru uloga od $100, uz kamatu od 12% na 5 godina:
Ako diskontiramo godišnje, kao do sad, tada nam formula izgleda ovako:
100*(1 + 0,12)^5
Imamo “na petu” jer je trajanje 5 godina.
Ako bismo uz iste uvjete imali polugodišnje diskontiranje, tada bismo u tih 5 godina diskontirali 10 puta tj. dva puta godišnje, u trajanju od pet godina.
ALI
kamata koju diskontiramo na polugodišnjem nivou nije 12%, već pola od toga, dakle 6%, ili 0.6.
Stoga formula ide ovako:
100*(1 + 0,06)^10
I sad je sve jasno. Tromjesečno je:
100*(1 + 0,03)^20
I mjesečno:
100*(1 + 0,01)^60
Efektivna i nominalna kamatna stopa
U prethodnom smo poglavlju vidjeli da je kamatu moguće obračunavati i češće od jednom godišnje.
Ako je kamata na kreditnoj kartici 3% mjesečno, tada je nominalna kamatna stopa 3*12=36%. (Ovako izračunata kamatna stopa zove se nominal Annualised Percentage Rate, ili APR.)
Ali zbog efekta kamate na kamatu, stvarnu kamatnu stopu može prikazati samo efektivna kamatna stopa, tj. Effective Annual Rate. ili EAR. (Ponekad Annual Equivalent Rate, ili AER).
Drugi primjer može bit da dvije različite banke prikazuju istu nominalnu kamatnu stopu na štednju od recimo 5%, a na kraju jedna ipak daje više novca od druge.
Razlika ovisi i o troškovima kredita, ali to sad nije tema. Pitanje, je koliko puta godišnje se obračunava tih 5%? Jednom, dvaput, četiri puta?
Recimo da prva banka na 1000 € daje kamatu od 5%, i obračunava je godišnje.
Jednostavno. Kamata se pripisuje tek na kraju godine, i na računu ćemo nakon godinu dana imati 1.050 €.
Druga banka također daje 5% na 1000 €, ali kamatu obračunava kvartalno, tj. četiri puta godišnje.
Može se naslutiti da će ova banka isplatiti više novca na kraju godine od prve, zbog češćeg obračuna kamate. (Ako su ostali parametri jednaki).
Naime, nakon prvog kvartala, dobit ćemo 1/4 kamate od 5%, a to je 0,25%, dakle 1000 € množimo s 1.0125.
Nakon tri mjeseca, tj. nakon prvog kvartala imamo 1012,5 €.
Nakon toga slijedi period od trećeg do šestog mjeseca, ali ovaj put kamatu od 0,25% [za drugi kvartal] više ne pripisujemo na 1000 € već na 1025 €, zato što je upravo to iznos kojeg imamo na početku trećeg mjeseca, budući da banka kamatu obračunava svaka tri mjeseca. I tako redom do pune godine, odnosno do 4 puta obračunate kamate.
Razlika između prve i druge banke u ovom slučaju nije dramatična. Prva na kraju godine daje 1.050,00 € a druga 1.050,95 €.
Kad ovih 50,95 € dobivenih u drugoj banci podijelimo s inicijalnih 1.000,00 €, dobit ćemo EAR od 0,05095, tj. 5,095%, što je više od nominalnih 5%.
S druge strane, ako su nam poznati podaci kolika je nominalna kamata i broj koliko se puta godišnje obračunava, EAR se dobiva iz sljedeće formule:
Formula: nominalna i efektivna kamatna stopa
Ovdje je “k” nominalna kamatna stopa, a “m” broj koliko se puta obračunava kamata.
Vremenska vrijednost novca – zaključak
Iz iskustva znam da ponekad jednostavne stvari mogu izgledati vrlo komplicirane. Jednom prilikom sam proveo nekoliko dana u društvu top menadžera iz poznatih hrvatskih kompanija, gledajući kako su se pogubili u prvih sat vremena predavanja o korporativnim financijama, i više nisu mogli uhvatiti priključak sve do kraja, samo zato što im temeljni koncept vremenske vrijednosti novca nije sjeo kako treba.
Upravo iz tog razloga sam odlučio napisati ovaj članak u pokušaju da što jasnije razložim ovu temu, istovremeno pomažući svima koji od ovakvih kalkulacija imaju koristi.
Ako ste student koji će uskoro slušati modul o korporativnim financijama, toplo vam savjetujem da prethodno dobro ovladate TVM konceptom, i modul će biti užitak. [Ok, možda neće ;)].
Potražite zadatke iz TVM, riješite ih gomilu dok sve ne sjedne na svoje mjesto, a onda vam savjetujem da si priuštite neki od financijskih kalkulatora kao što je HP 10B2 koji će vas vjerno pratiti kad god na brzinu treba izračunati NPV ili IRR nekog projekta. Ms Excel također ima sve potrebne formule, kao što su NPer, PV, PMT, FV, NPV, IRR…
Ako mislite da nešto treba dodati (ili oduzeti), bit će mi drago družiti se u komentarima. Vidimo se u nekom drugom članku!


Super objašnjeno. Hvala!
Hvala Gorane!
Hvala!
Bilo mi je zadovoljstvo!
Odličan članak. I za laike i za profesionalce.
@Nikola, hvala Vam na komentaru. Drago mi je da vam je članak koristan.
Molim vas kolika bi bila danasnja vrijednost u kunama 2500 njemackih maraka 1992g.
Poštovani Krsto, vrijednost bi bila 1.949,21€. 🙂